Special Properties of Linearity

Special Properties of Linearity

Linearity is commutative, a property including the blend of at least two frameworks. Figure 5-10 shows the general thought. Envision two frameworks joined in a course, that is, the yield of one framework is the contribution to the following. On the off chance that every framework is direct, at that point the general mix will likewise be straight.

 The commutative property expresses that the request for the frameworks in the course can be revised without influencing the attributes of the general mix. You likely have utilized this guideline in electronic circuits. For instance, envision a circuit made out of two phases, one for enhancement, and one for separating. Which is ideal, enhance and afterward channel, or channel and afterward intensify? On the off chance that the two phases are direct, the request doesn't have any effect and the general outcome is the equivalent. Remember that genuine hardware has nonlinear impacts that may make the request significant, for example: impedance, DC balances, inside clamor, slew rate bending, and so on.

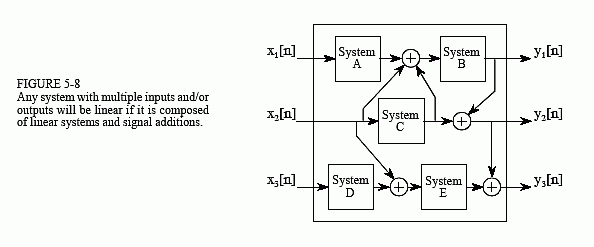
Figure 5-8 shows the subsequent stage in straight framework hypothesis: numerous information sources and yields. A framework with numerous sources of info and additionally yields will be straight on the off chance that it is made out of direct subsystems and options of signs. The multifaceted nature doesn't make a difference, just that nothing nonlinear is permitted within the framework. 

To comprehend what linearity implies for frameworks with numerous data sources as well as yields, consider the accompanying psychological study. Start by putting a sign on one information while different data sources are held at zero.

 This will make the numerous yields react with some example of signs. Next, rehash the technique by putting another sign on an alternate information. Similarly as in the past, keep the entirety of different contributions at zero. 

This subsequent information sign will bring about another example of signs showing up on the various yields. To complete the trial, place the two signs on their separate data sources at the same time.

 The signs showing up on the yields will basically be the superposition (aggregate) of the yield signals delivered when the info signals were applied independently.

The utilization of increase in straight frameworks is every now and again misjudged. This is on the grounds that augmentation can be either straight or nonlinear, contingent upon what the sign is duplicated by. Figure 5-9 outlines the two cases. A framework that duplicates the info signal by a consistent, is direct.

 This framework is an enhancer or an attenuator, depending if the consistent is more prominent or short of what one, separately. Interestingly, increasing a sign by another sign is nonlinear. Envision a sinusoid increased by another sinusoid; the subsequent waveform is plainly not sinusoidal. 

Another generally misjudged circumstance identifies with parasitic signs included hardware, for example, DC counterbalances and warm commotion. Is the expansion of these superfluous signs straight or nonlinear?

 The appropriate response relies upon where the tainting signals are seen as starting. In the event that they are seen as originating from inside the framework, the procedure is nonlinear.

 

This is on the grounds that a sinusoidal information doesn't deliver an unadulterated sinusoidal yield. Alternately, the incidental sign can be seen as remotely entering the framework on a different contribution of a numerous info framework. 

This makes the procedure straight, since just a sign expansion is required inside the framework.