Requirements for Linearity

Requirements of Linearity

A framework is called direct on the off chance that it has two scientific properties: homogeneity and additivity. In the event that you can show that a framework has the two properties, at that point you have demonstrated that the framework is direct. In like manner, in the event that you can show that a framework doesn't have one or the two properties, you have demonstrated that it isn't direct. A third property, move invariance, is definitely not a severe prerequisite for linearity, however it is an obligatory property for most DSP procedures. At the point when you see the term direct framework utilized in DSP, you ought to accept it incorporates move invariance except if you have motivation to accept something else. These three properties structure the science of how direct framework hypothesis is characterized and utilized. Later in this section we will take a gander at increasingly natural methods of getting linearity. Until further notice, how about we experience these formal scientific properties.

As represented in Fig.(5.1) homogeneity implies that an adjustment in the info sign's sufficiency brings about a relating change in the yield sign's adequacy. In scientific terms, if an information sign of x[n] brings about a yield sign of y[n], a contribution of kx[n] brings about a yield of ky[n], for any info sign and steady, k.

A straightforward resistor gives a genuine case of both homogenous and non-homogeneous frameworks. In the event that the contribution to the framework is the voltage over the resistor, v(t), and the yield from the framework is the current through the resistor, i(t) , the framework is homogeneous. Ohm's law ensures this; if the voltage is expanded or diminished, there will be a relating increment or abatement in the current. Presently, consider another framework where the info signal is the voltage over the resistor, v(t), yet the yield signal is the force being scattered in the resistor, p(t). Since power is relative to the square of the voltage, if the info signal is expanded by a factor of two, the yield signal is increment by a factor of four. This framework isn't homogeneous and accordingly can't be straight. 

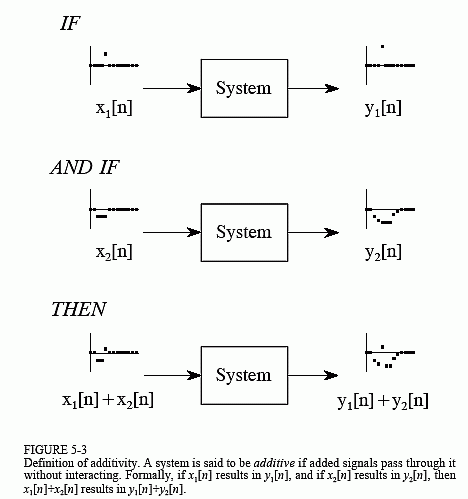
The property of additivity is delineated in Fig. 5-3. Consider a framework where a contribution of x1[n] produces a yield of y1[n]. Further guess that an alternate information, x2[n], produces another yield, y2[n]. The framework is supposed to be added substance, if a contribution of x1[n] + x2[n] brings about a yield of y1[n] + y2[n], for all conceivable information signals. In words, signals included at the information produce flags that are included at the yield.

The significant point is that additional signs go through the framework without associating. For instance, consider a phone discussion with your Aunt Edna and Uncle Bernie. Auntie Edna starts a somewhat extensive tale about how well her radishes are getting along this year. Out of sight, Uncle Bernie is shouting at the canine for having a mishap in his preferred seat. The two voice signals are included and electronically transmitted through the phone organize. Since this framework is added substance, the sound you hear is the total of the two voices as they would sound whenever transmitted independently. You hear Edna and Bernie, not the animal, Ednabernie. 

A genuine case of a nonadditive circuit is the blender stage in a radio transmitter. Two signs are available: a sound sign that contains the voice or music, and a transporter wave that can spread through space when applied to a reception apparatus. The two signs are added and applied to a nonlinearity, for example, a pn intersection diode. This outcomes in the signs converging to frame a third sign, a tweaked radio wave equipped for conveying the data over significant stretches. 

As appeared in Fig. 5.4, move invariance implies that a move in the info sign will bring about simply an indistinguishable move in the yield signal. In progressively formal terms, if an information sign of x[n] brings about a yield of y[n], an information sign of x[n + s] brings about a yield of y[n + s], for any information signal and any steady, s. Pay specific notification to how the science of this move is composed, it will be utilized in up and coming sections. By including a steady, s, to the free factor, n, the waveform can be progressed or hindered in the flat course. For instance, when s = 2, the sign is moved left by two examples; when s = - 2, the sign is moved right by two examples.

Move invariance is significant in light of the fact that it implies the attributes of the framework don't change with time (or whatever the free factor happens to be). On the off chance that a blip in the info causes a blop in the yield, you can be guaranteed that another blip will cause an indistinguishable blop. The greater part of the frameworks you experience will be move invariant. This is blessed, in light of the fact that it is hard to manage frameworks that change their qualities while in activity. For instance, envision that you have planned a computerized channel to make up for the corrupting impacts of a phone transmission line. Your channel makes the voices sound increasingly characteristic and more clear. Causing you a deep sense of shock, along comes winter and you discover the qualities of the phone line have changed with temperature. Your pay channel is presently jumbled and doesn't work particularly well. This circumstance may require a progressively modern calculation that can adjust to evolving conditions. 

For what reason do homogeneity and additivity assume a basic job in linearity, while move invariance is something as an afterthought? This is on the grounds that linearity is an extremely wide idea, enveloping considerably more than just signals and frameworks. For instance, consider a rancher selling oranges for $2 per box and apples for $5 per container. In the event that the rancher sells just oranges, he will get $20 for 10 boxes, and $40 for 20 containers, making the trade homogenous. On the off chance that he sells 20 cartons of oranges and 10 containers of apples, the rancher will get: . This is a similar sum as though the two had been sold independently, making the exchange added substance. Being both homogenous and added substance, this offer of merchandise is a straight procedure. Be that as it may, since there are no signs included, this isn't a framework, and move invariance has no importance. Move invariance can be thought of as an extra part of linearity required when signs and frameworks are included.